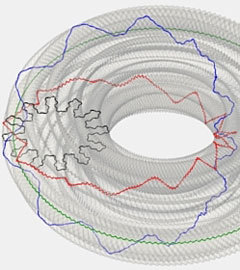
Математики вперше
показали зображення плоского тора - абстрактної математичної фігури, вперше
передбаченої математиками Ніколасом Кейпером та нобелівським лауреатом Джоном
Нешем в середині минулого століття. Робота опублікована в журналі Праці
Національної академії наук, її короткий опис можна прочитати на сайті
французького Національного центру наукових досліджень.
Плоский тор - це
фігура, топологічно еквівалентна квадрату. Якщо уявити собі квадрат і з'єднати
його верхню межу з нижньою, ми отримаємо щось подібне до циліндра. Якщо потім
з'єднати краї циліндра один з одним, то вийде тор - фігура, схожа на бублик.
Однак, якщо на вихідний квадрат нанести вертикальні і горизонтальні лінії, то
вертикальні лінії в ході перетворення збережуть свою довжину, в той час як
горизонтальні виявляться розтягнутими. Це відбувається тому, що неможливо
поєднати краї циліндра, не розтягуючи його.
Неш і Кейпер в
середині п'ятдесятих років минулого століття довели існування такого тора в
тривимірному просторі, в якому ні горизонтальні, ні вертикальні лінії не будуть
розтягнуті (в чотиривимірному такий тор будується досить просто). Таку фігуру
називали плоским тором. Пізніше, в 70-80ті роки радянський математик Михайло
Громов розробив метод, який міг допомогти побудувати таку фігуру. Французьким
математикам вдалося розробити на основі методу Громова алгоритм, який дозволив
отримати зображення фігури.
Алгоритм діяв
так. Він починав зі звичайного гладкого тора і м'яв його так, щоб вертикальні
лінії вихідного квадрата наблизилися по довжині до розтягнутих горизонтальних.
Отримана
комп'ютерна тривимірна модель складалася з майже двох мільярдів вузлів.
Обрисами вона нагадувала тор, хоча і мала незвичайні властивості. Поверхня
моделі була періодичною (самоподібною), і цим нагадувала поверхню фракталів,
але при цьому, на відміну від фракталів, все одно залишалася гладкою. |







